Summary
In this article I will add a new task to the AnyCloud BLE Advertising Scanning application which will save the advertising data into a database.
Story
There is still a boatload of mostly unintelligible advertising data coming ripping onto our screen. It is FINALLY time to start fixing that. In this article I will create a new task called the advertising database task which will hold the history of advertising packets that I have seen. I will update the Bluetooth Manager task to submit the advertising packets to a queue running in the advertising database task.
There are
| Article | Topic |
|---|---|
| AnyCloud Bluetooth Advertising Scanner (Part 1) | Introduction to AnyCloud Bluetooth Advertising |
| AnyCloud Bluetooth Advertising Scanner (Part 2) | Creating an AnyCloud Bluetooth project |
| AnyCloud Bluetooth Advertising Scanner (Part 3) | Adding Observing functionality to the project |
| AnyCloud Bluetooth Utilities Library | A set of APIs for enhancement of the AnyCloud Library |
| AnyCloud Bluetooth Advertising Scanner (Part 4) | Adding a command line to the scanner |
| AnyCloud Bluetooth Advertising Scanner (Part 5) | Adding a history database to the scanner |
| AnyCloud Bluetooth Advertising Scanner (Part 6) | Decoding advertising packets |
| AnyCloud Bluetooth Advertising Scanner (Part 7) | Adding recording commands to the command line |
| AnyCloud Bluetooth Advertising Scanner (Part 8) | Adding filtering to the scanner |
| AnyCloud Bluetooth Advertising Scanner (Part 9) | Improve the print and add packet age |
| AnyCloud Bluetooth Advertising Scanner (Part 10) | Sort the database |
All of the code can be found at git@github.com:iotexpert/AnyCloudBLEScanner.git and https://github.com/iotexpert/AnyCloudBLEScanner.git
There are git tags in place starting at part 5 so that you can look at just that version of the code. "git tag" to list the tags. And "git checkout part6" to look at the part 6 version of the code.
You can also create a new project with this is a template if you have the IoT Expert Manifest Files installed
Create an Advertising Data Database Task
We need to create the file advertisingDatabase.h which will hold the task prototype (so that main can get going).
#pragma once void adb_task(void *arg);
Then create the advertisingDatabase.c to hold the actual database code. It will start with the definition of messages which can be sent to the task. For now just “ADB_ADD”. To make things a little bit simpler these command can have two data elements (which I call data0 and data1). Then the main part of the task just
- Creates the queue to manage the messages
- Process the message until the end of time
#include "FreeRTOS.h"
#include "queue.h"
static QueueHandle_t adb_cmdQueue;
typedef enum {
ADB_ADD,
} adb_cmd_t;
typedef struct
{
adb_cmd_t cmd;
void *data0;
void *data1;
} adb_cmdMsg_t;
void adb_task(void *arg)
{
// setup the queue
adb_cmdMsg_t msg;
adb_cmdQueue = xQueueCreate(10,sizeof(adb_cmdMsg_t));
while(1)
{
BaseType_t status = xQueueReceive(adb_cmdQueue,&msg,portMAX_DELAY);
if(status == pdTRUE)
{
switch(msg.cmd)
{
case ADB_ADD:
break;
}
}
}
}
To start the task, you need to add it to main.c.
xTaskCreate(adb_task,"adv database",configMINIMAL_STACK_SIZE*4,0,1,0);
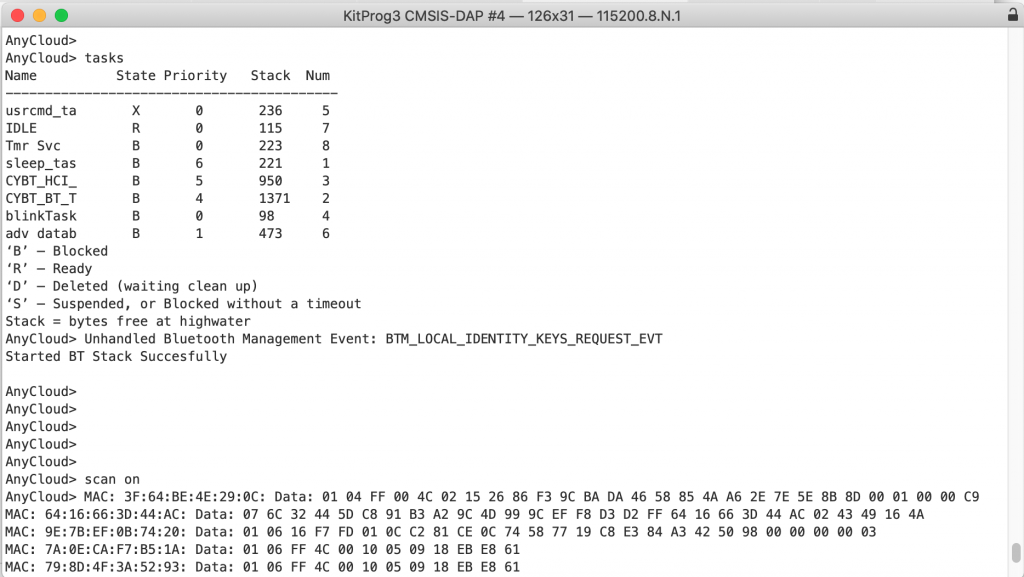
When I build and program this, you can now see the new task. Good that working.
AnyCloud> Unhandled Bluetooth Management Event: BTM_LOCAL_IDENTITY_KEYS_REQUEST_EVT Started BT Stack Succesfully AnyCloud> tasks Name State Priority Stack Num ------------------------------------------ usrcmd_ta X 0 228 5 IDLE R 0 115 7 Tmr Svc B 0 223 8 CYBT_HCI_ B 5 950 3 sleep_tas B 6 221 1 CYBT_BT_T B 4 1371 2 blinkTask B 0 98 4 adv datab B 1 479 6 ‘B’ – Blocked ‘R’ – Ready ‘D’ – Deleted (waiting clean up) ‘S’ – Suspended, or Blocked without a timeout Stack = bytes free at highwater AnyCloud>
Update the Advertising Database to Accept Submitted ADV Packets
If you recall our original setup was to take advertising packets in the Bluetooth Manager thread and print out the data. The first thing that we want to fix up is the ability of the advertising database task to accept advertising packets which are pushed to its command queue. To prepare for this I create two local variables to hold the data.
void adb_task(void *arg)
{
// setup the queue
adb_cmdMsg_t msg;
wiced_bt_ble_scan_results_t *scan_result;
uint8_t *data;
Then I update the ADB_ADD command. My first, and really simple fix, is to grab the printing code from the Bluetooth Manager task. Obviously this won’t be an improvement from the original program as far as the users goes, but it will verify that the tasks are working properly together.
case ADB_ADD:
// Print the MAC Address
scan_result = (wiced_bt_ble_scan_results_t *)msg.data0;
data = (uint8_t *)msg.data1;
printf("MAC: ");
for(int i=0;i<BD_ADDR_LEN;i++)
{
printf("%02X:",scan_result->remote_bd_addr[i]);
}
// Print the RAW Data of the ADV Packet
printf(" Data: ");
int i=0;
while(data[i])
{
for(int j=0;j<data[i];j++)
{
printf("%02X ",data[i+1+j]);
}
i = i + data[i]+1;
}
printf("\n");
free(msg.data0);
free(msg.data1);
break;
Then I add a command to the advertisingDatabase.h which the Bluetooth Manager task can call to submit advertising packets
void adb_addAdv(wiced_bt_ble_scan_results_t *scan_result,void *data);
The actual command in advertisingDatabase.c just takes the advertising information, puts it in a command message, then submits it to the command queue.
void adb_addAdv(wiced_bt_ble_scan_results_t *scan_result,void *data)
{
adb_cmdMsg_t msg;
msg.cmd = ADB_ADD;
msg.data0 = (void *)scan_result;
msg.data1 = (void *)data;
xQueueSend(adb_cmdQueue,&msg,0); // If you loose an adv packet it is OK...
}
Update the Bluetooth Manager to Submit Adv Packets
Now I go and edit the bluetoothManager. c to submit packets rather than print them. To do this I greatly simplify the callback. There is one VERY important issue to deal with, which is one of those potential religious war issues. Memory.
When you get the callback from the stack, it gives you POINTERS to data for the advertising packet that reside inside of buffers inside of the stack. As soon as this callback returns this memory is purged. To prevent this data from getting cleaned up by the stack I
- Malloc some memory for the wiced_bt_ble_scan_results
- Malloc some memory for the advertising data
- Make a copy of the data
- Submit it to the Advertising Database
I KNOW from the spec that the largest data packet is 31-bytes (actually it is 31-bytes + one more field with length 0). So I know the maximum length is 32-bytes This means that in many situations I will be copying GARBAGE into my buffer if the packet is less than 32 bytes long. I think that this is simpler than calculating the length and then only copying that much data.
void btm_advCallback(wiced_bt_ble_scan_results_t *p_scan_result, uint8_t *p_adv_data)
{
wiced_bt_ble_scan_results_t *scan_result = malloc(sizeof(wiced_bt_ble_scan_results_t));
uint8_t *data = malloc(32);
memcpy(data,p_adv_data,32);
memcpy(scan_result,p_scan_result->remote_bd_addr,BD_ADDR_LEN);
adb_addAdv(scan_result,data);
}
When I run this updated program I should get the same stream of data coming out on the serial port. Sure enough the new thread is working.
Create an Advertising Data Database
Now, lets create an actual database. To simplify things my database is just an array of structures. One structure per bluetooth device. The structure will contain a pointer to the information about the device it just saw and the actual raw data.
typedef struct {
wiced_bt_ble_scan_results_t *result;
uint8_t *data;
} adb_adv_t ;
#define ADB_MAX_SIZE (40)
adb_adv_t adb_database[ADB_MAX_SIZE];
int adb_db_count=0;
Then I will create several helper functions to work with the database
- Find devices in the database given a mac address
- Print an entry in the database
- Add entries to the database
First, find an entry in the database. This function will search through the database and compare the mac address against the mac address in the database. When the memcmp ==0 meaning it found a match, it will return that entry.
static int adb_db_find(wiced_bt_device_address_t *add)
{
int rval=-1;
for(int i=0;i<adb_db_count;i++)
{
if(memcmp(add,&adb_database[i].result->remote_bd_addr,BD_ADDR_LEN)==0)
{
rval = i;
break;
}
}
return rval;
}
The print function will make sure that you asked for a legal entry (much must be greater than 0… and less than the max). Then it will print out the mac address and the raw data. In a future post I will add a smarter print out.
static void adb_db_printEntry(int entry)
{
if(!(entry>= 0 && entry <= adb_db_count))
{
printf("Illegal entry\n");
return;
}
printf("%02d MAC: ",entry);
for(int i=0;i<BD_ADDR_LEN;i++)
{
printf("%02X:",adb_database[entry].result->remote_bd_addr[i]);
}
// Print the RAW Data of the ADV Packet
printf(" Data: ");
int i=0;
while(adb_database[entry].data[i])
{
for(int j=0;j<adb_database[entry].data[i];j++)
{
printf("%02X ",adb_database[entry].data[i+1+j]);
}
i = i + adb_database[entry].data[i]+1;
}
printf("\n");
}
To add an entry to the database, first make sure that it isn’t already in the database. Then when you are sure that it isn’t the database, you just add the pointers to your table. You need to make sure and not go beyond the end of the table, and if you did, you will have effectively blown away the last entry in the table. Oh well.
static void adb_db_add(wiced_bt_ble_scan_results_t *scan_result,uint8_t *data)
{
int entry = adb_db_find(&scan_result->remote_bd_addr);
if(entry == -1)
{
adb_database[adb_db_count].result = scan_result;
adb_database[adb_db_count].data = data;
adb_db_printEntry(adb_db_count);
adb_db_count = adb_db_count + 1;
if(adb_db_count == ADB_MAX_SIZE)
{
printf("ADV Table Max Size\n");
adb_db_count = adb_db_count - 1;
}
}
else
{
free(scan_result);
free(data);
}
}
Add a Command to Print the Database
Now we want to add the ability to print from the command line. So add a new command message to the list of legal commands.
typedef enum {
ADB_ADD,
ADB_PRINT,
} adb_cmd_t;
Then create a new function to print. If you send in a “-1” it will print the whole table. Otherwise just print the individual entry.
static void adb_printTable(int entry)
{
if(entry == -1)
{
for(int i=0;i<adb_db_count;i++)
{
adb_db_printEntry(i);
}
}
else
{
adb_db_printEntry(entry);
}
}
Now edit usercmd.c to have the new command line. Notice that I use “sscanf” which obviously has some issues. Too bad.
static int usrcmd_print(int argc, char **argv)
{
if(argc == 1)
{
adb_print(-1); // Print whole table
}
if(argc == 2)
{
int val;
sscanf(argv[1],"%d",&val);
adb_print(val);
}
return 0;
}
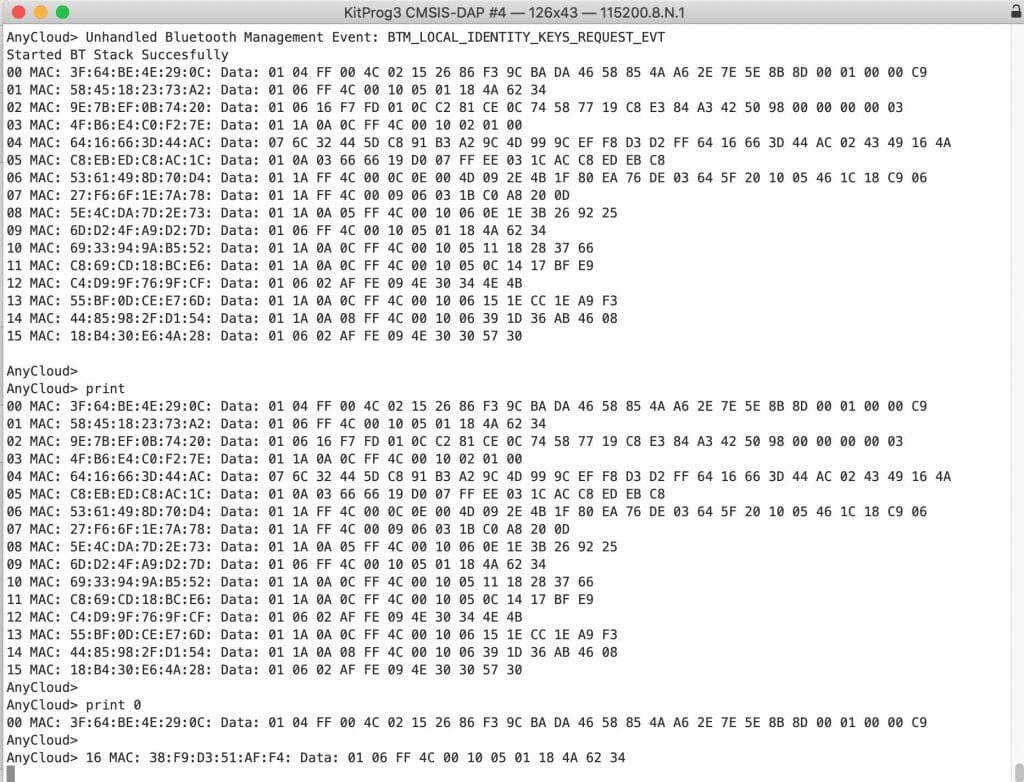
When I program the project it immediately prints out a bunch of devices that are at my house. Then you can see I run the “print” command which prints the table. Finally P do a print 0 to just print the first entry.
In the next article I will add smarter diagnostics to the advertising packets.


No comment yet, add your voice below!