Keithley 2380-500-15 & 2380-120-60

Summary

In this article I discuss my ridiculous motivation for buying a new Keithley 2830-120-60 to replace my very functional Keithey 2380-500-15

2380-500-15 & 2380-120-60

While working on the IRDC3894 I spent a significant amount of time using the Keithley 2380 in Constant Current Mode.  The development kit that I was testing was configured to enable 1.2v output at 15A.  In the picture below I am pulling 1A.  You can see the Keithley set to pull 1A and it is actually drawing 0.9998A (plenty close)

While I was testing the setup I would slowly increase the current.  In the picture below you can see that I got to 5.4A with no problem.

But at 5.5A the trouble starts.  In the picture below you can see that I am asking for 5.5A but I am only getting 5.48A

And the gap gets worse as I increase the current.

So I posted on the Keithley site trying to figure out what was happening.  Was the Keithley dead?

And unfortunately there is the answer.  The load has a minimum operating voltage of 4.5v when it is in the 15A mode.

But the 2380-120-60 has a 1.8V operating voltage at 60A

And when I get it plugged in I find that it will happily deliver 16A at 1.2V

And it doesn’t start to roll over until 17A (at 1.2V)

Infineon SupIRbuck – Low Voltage/High Current Measurement

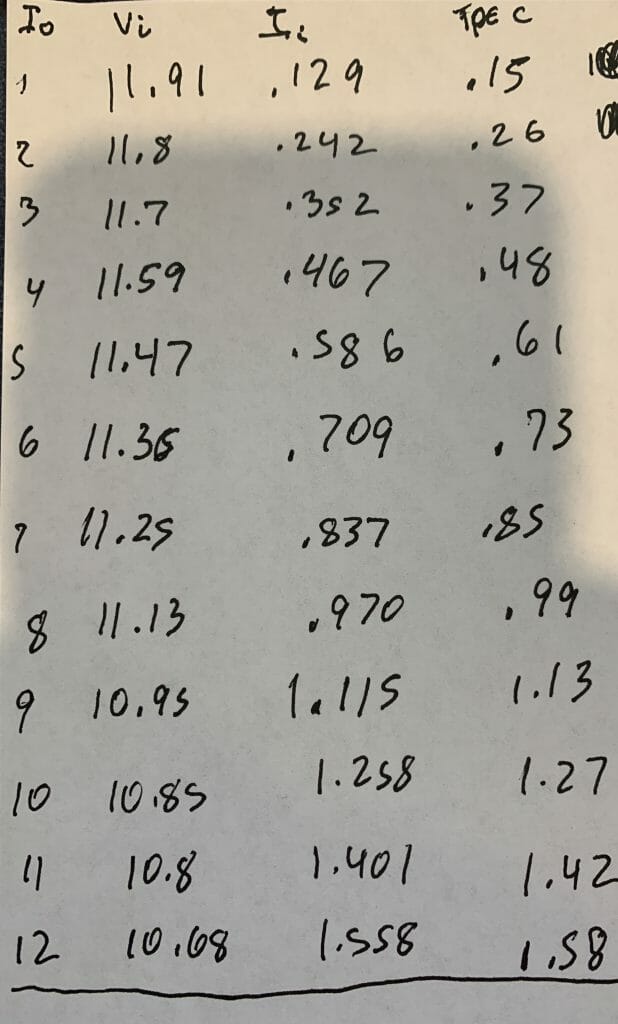
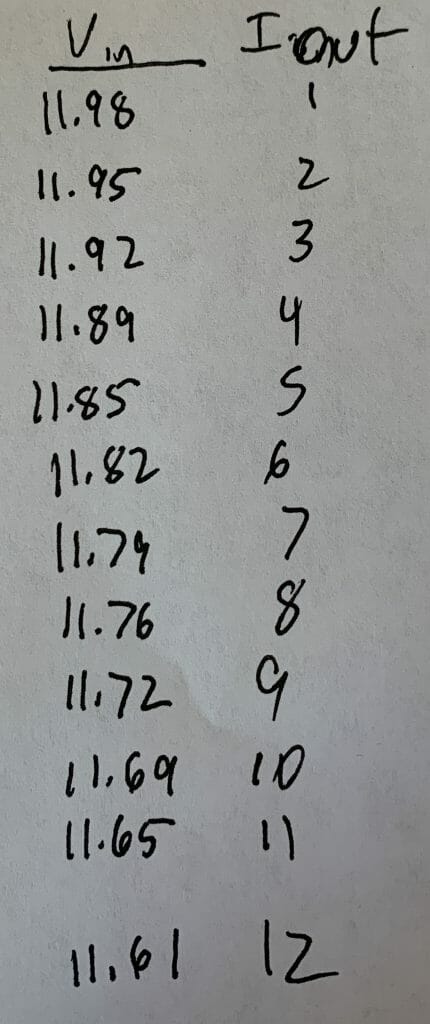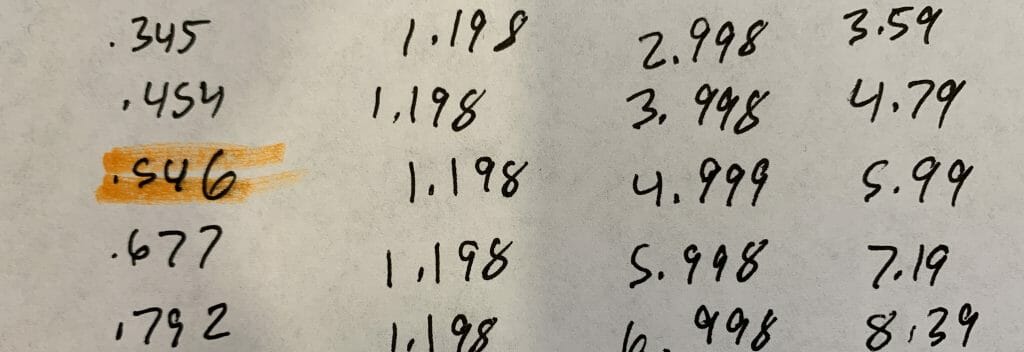Summary

This article will show you the steps to produce 12A from and IRDC3894.  It also discusses low voltage high current measurement and burden voltage.

The Story

In the last few weeks I have been working on a TypeC to Infineon SupIRbuck power supply that will turn 20V@3A into 5V@12A.

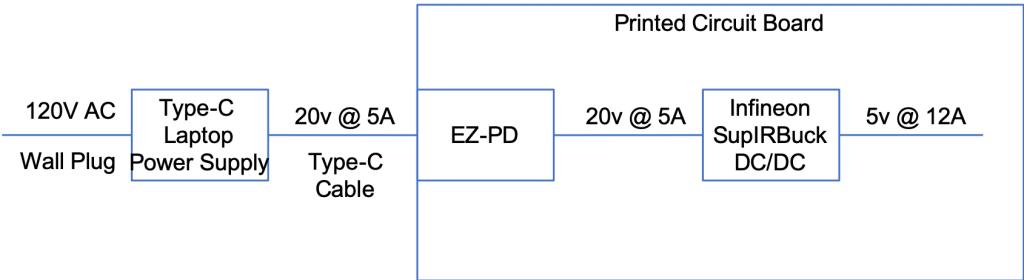
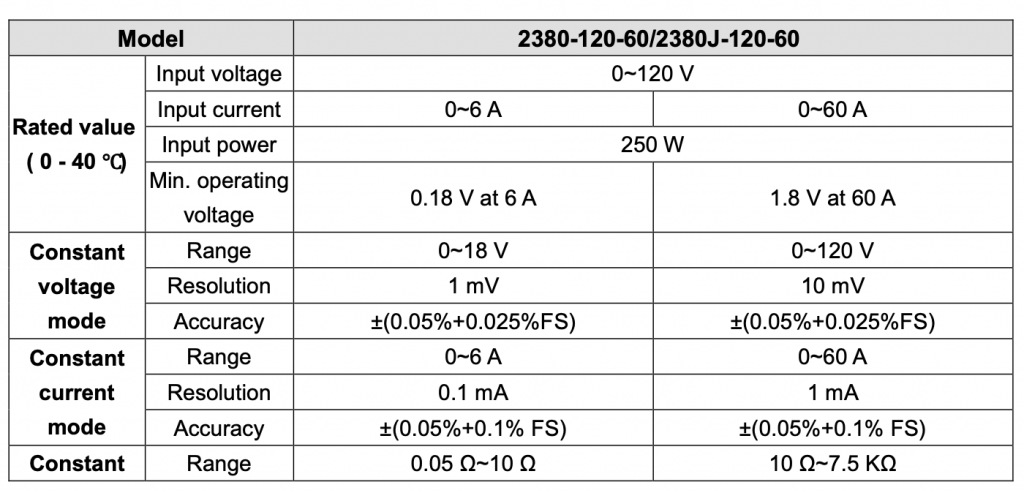
In that process I have been working with a Keithley 2380-500-15 which can act as a load simulator for my design.  The 15 in name means that it can pull 15A which should be more an adequate to test my design.  Unfortunately when I was looking at the specs, I read the part about “15A” but not the part about the “Min Operating Voltage in the 15A range = 4.5V”

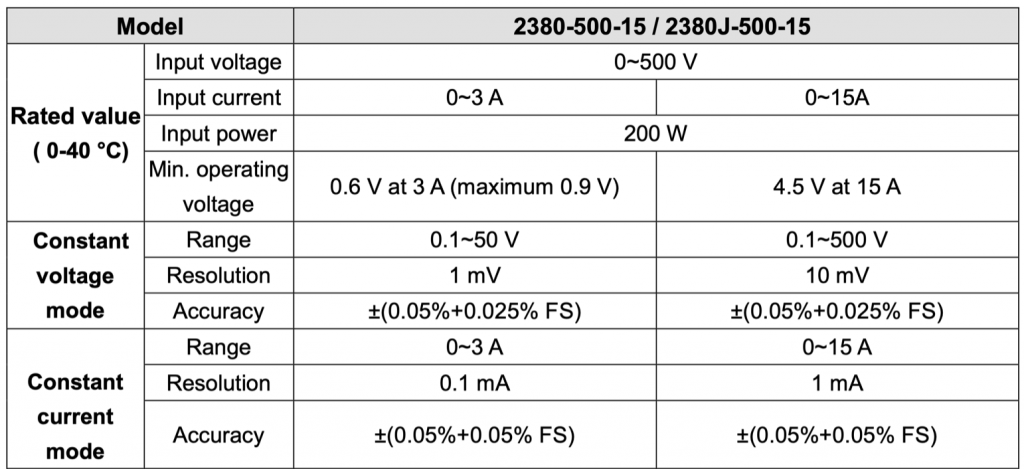
And what I really should have bought (and now have) is a 2380-120-60

Big Resistors

But I really wanted to be able to measure the current coming out of the IR3894.  So, I decided to buy some “Big” resistors.  Well they are not actually high resistance, but they are HIGH power. 35W and 50W.  Unfortunately they are also $4 each.  Here is a 0.33Ω 50W resistor.  (I will totally understand the value of that giant heat sink later on in this article)

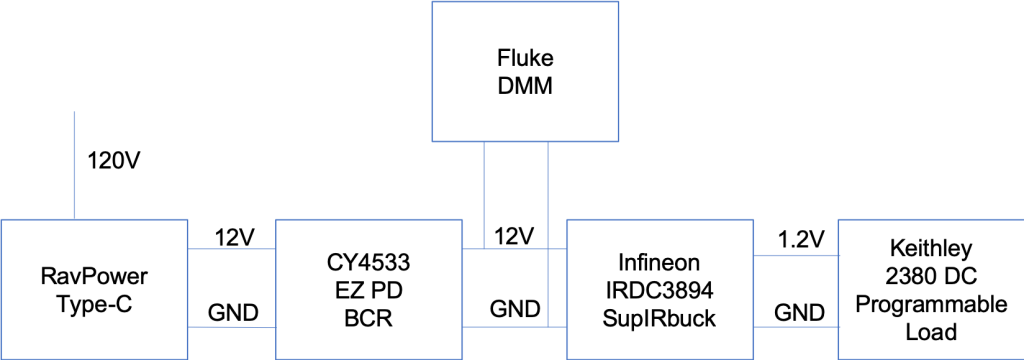
My measurement setup looks like this:

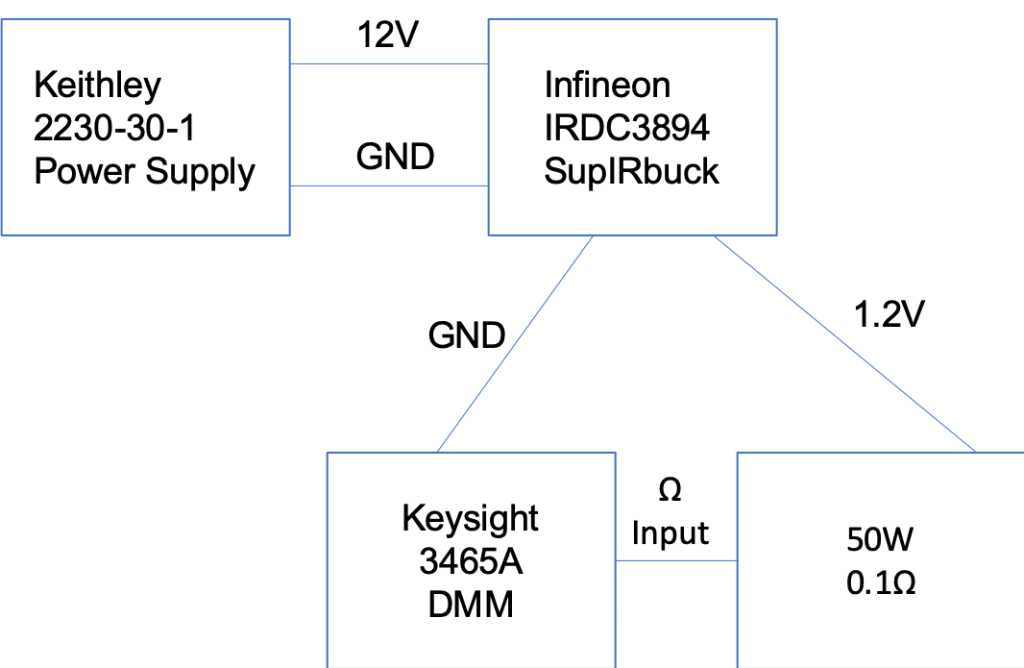
And actually looks like this terrible mess:

Start the measurements

I bought 7 different resistors ranging from 0.1Ω to 1Ω.  This means that I should be able to get something like this table.  Note that the 0.1Ω is marked in red because it exceeds the current limit of my multimeter. (i.e. don’t do that)

V R A W Rating
1.2 0.10 12.0 14.4 35
1.2 0.15 8.0 9.6 50
1.2 0.20 6.0 7.2 35
1.2 0.33 3.6 4.4 50
1.2 0.50 2.4 2.9 35
1.2 0.75 1.6 1.9 50
1.2 1.00 1.2 1.4 50

I wasn’t exactly sure what was going to happen so I decided to start with the 0.33Ω resistor

I was hoping to get 1.2V/0.33Ω = 3.6A yet I end up with 1.99A where is my other 1.6A?

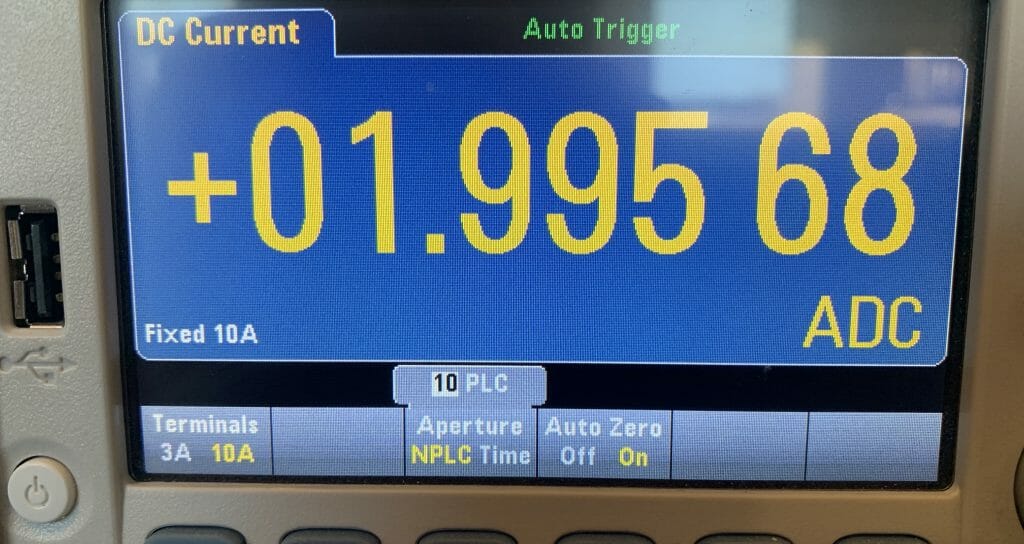
I put in a 0.1Ω, 0.15Ω and 0.75Ω and measured the current.  Then I calculate the effective resistance of the system and it turns out that there is essentially another 0.27Ω in series with my R1

V=I(R1+Rb)

V/I-R1 = Rb

V A R1Ω RbΩ R1+RbΩ
1.2 2.0 0.33 0.27 0.60
1.2 3.16 0.10 0.28 0.38
1.2 2.85 0.15 0.27 0.42
1.2 1.175 0.75 0.27 1.02

Where in the world is the other 0.27Ω?

Melt the Probe

This leads me to the great idea that is just the lead wires, and that I ought to just pull out the resistor and see what happens.  Well, what happens is that I melt the probe, and I still don’t get numbers that make sense.

Burden Voltage

The real story is, of course, that digital multimeters are hardly “ideal” and that when you are measuring current what you are really doing is measuring the voltage across a “shunt resistor”.  A shunt resistor is just a small valued highly precise resistor.  The voltage across this resistor is also known as the burden voltage (which is why I called it Rb above).  Here is a picture out of the Keysight documentation.

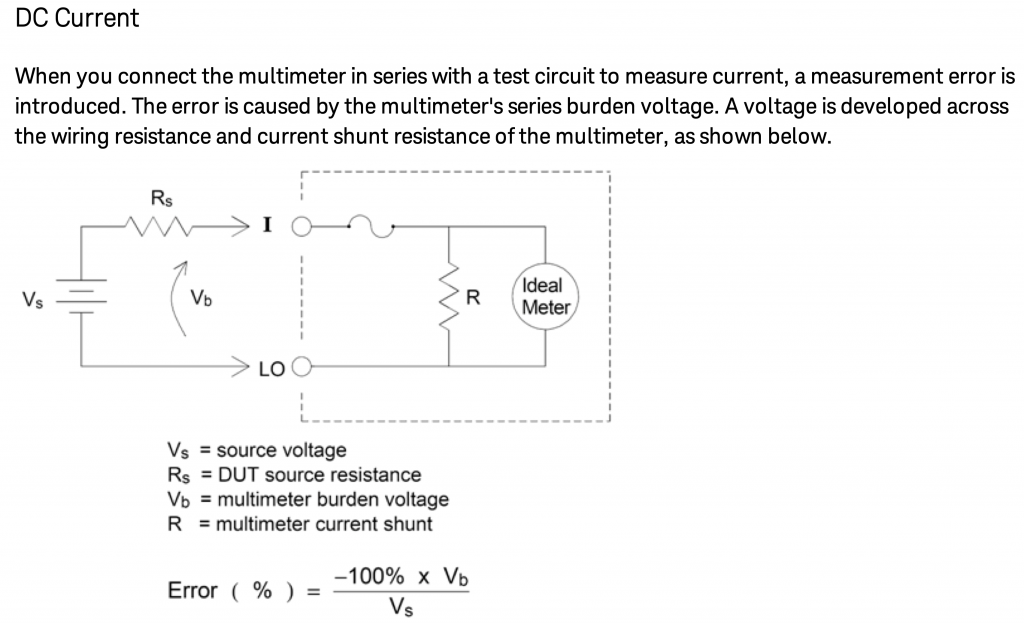
But how big is that resistor?  Well, unfortunately it is not specified directly in the documentation.  But, when you look at the data sheet you find that the maximum burden voltage is 0.5V at 10A.

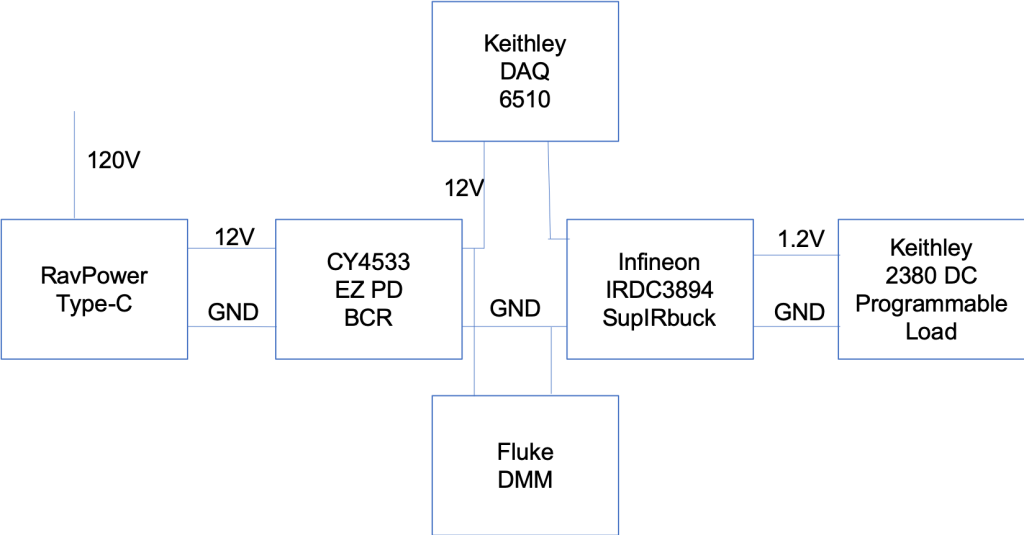
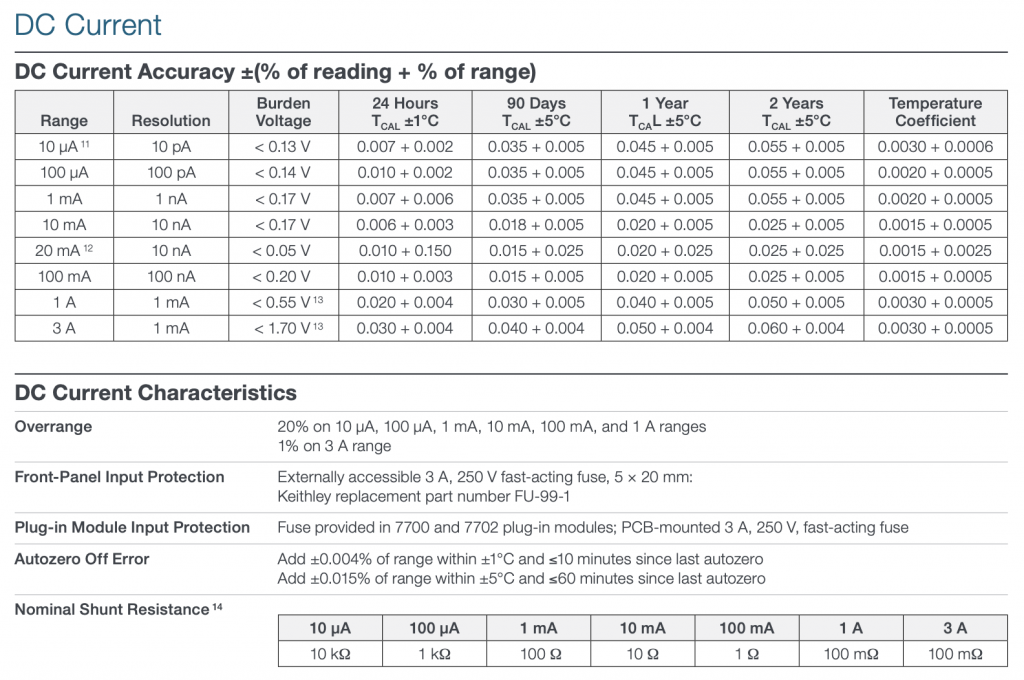
This means that shunt resistor is no more than 0.5v/10A=0.05Ω.  I just ordered a new Keithley DAQ6510 Digital Acquisition System Multimeter (which Im very excited about) that has the following table in documentation where it says the shunt resistor is 100mΩ for the 3A range.

Measure the Lead Resistance

So now we know that the shunt resistor is something like 0.05Ω.  That means the rest of the resistance has to be in the test setup.  So

V=(R1 + Rl + Rb)*I … the lead resistance + the shunt resistor + the actual resistor.  I go ahead and calculate what the lead resistance with several different resistors.

This means the resistance of my lead wires must be something like 0.23Ω

V A R1 Rl Rb R1+Rb+Rl VR1 VRl VRb
1.2 2.00 0.33 0.23 0.04 0.37 0.66 0.46 0.08
1.2 3.16 0.10 0.23 0.04 0.15 0.32 0.73 0.16
1.2 2.85 0.15 0.23 0.04 0.19 0.43 0.66 0.12
1.2 1.18 0.75 0.23 0.04 0.79 0.88 0.27 0.05

Again I start to look for the lead wire resistance … 0.6Ω for the melted lead.  Curious.

It is pretty easy to get some crazy measurements.  2.7Ω just pushing two banana plugs together (though you can see it blinking)

If I measure the red banana plug wire looped back the measurement is 0.016Ω – OK that is pretty small

And the black one is almost the same.

After some experimenting mixing and matching cables together the lowest I manage to get in a configuration that I can actually plug together is 0.15Ω which gave me 7.8A.

So where does this leave me?  To tell you the truth it leaves me a bit frustrated.  I really wanted to get 12A out of my setup (which is what it should be able to do).  But the most I can safely measure is 10A.  And the lowest combination of resistors I seem to be able to get is 0.15Ω.  So I decide to solder the 0.1Ω resistor straight into the board and see what happens. (yes that is some ugly soldering)

And now Im really frustrated because when I turn on the bench power supply I get 9.9V and 0.6A … even though it is set for 12V

And when I look at the output voltage I get 0.4V.  Which means it isn’t working.  Why?  I don’t know…. which is beyond annoying.  Walk away now I say to myself (actually that was my wife yelling at me 🙂 )

24 Hours Later

After sleeping on it, I remember that the Enable pin is used as an “Under Voltage Lock Out”.  The purpose of the UVLO is to not turn on until the input voltage has enough power to supply the system.  Given that I am am asking for 12A I realize… maybe I need to “enable” later in the power supply voltage rise.

So what I do I solder in a jumper to “Enable” then I press fit it into the ground.  Then turn on the power supply.  I measure the output as 0V.  That is good.  Then pull the enable jumper wire and let the IR3894 turn on.

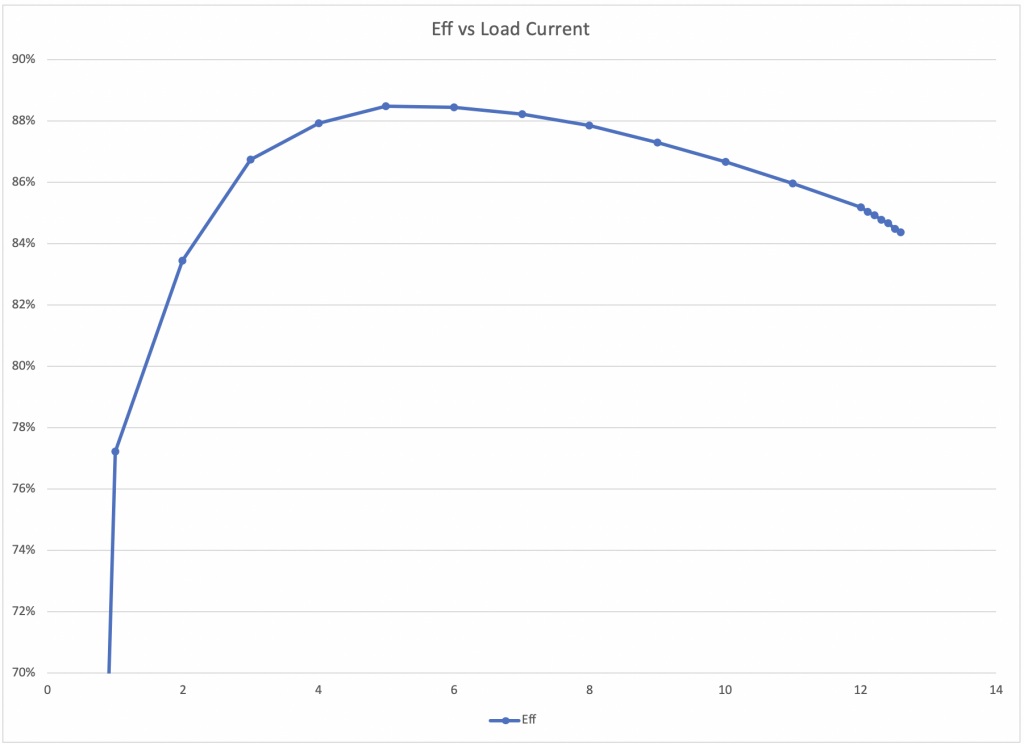
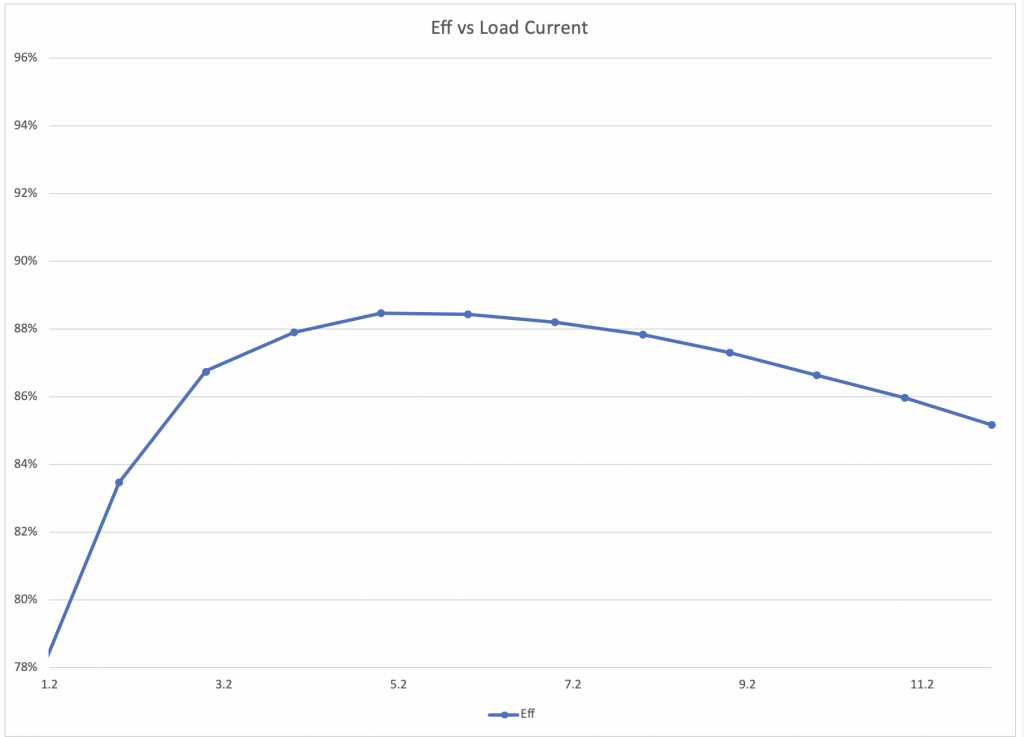
Sure enough.  When I look at the input it gets to 12V@1.4A and the output is still steady at 1.2v.  And my 0.1Ω is very hot.  I suppose that heatsink tab is there for a  reason.

I know from Ohms law that I am getting 12A@1.2V.  So the IR3894 seems to do the trick!

Cypress Type-C Barrel Connector Replacement + Infineon Buck DC/DC (Part 3)

Summary

This article walks you through the steps to test the CY4533 Type-C BCR & IR3894 under the load conditions from 1A to 12A.  In the previous article, I supplied power to the IR3894 using a bench top power supply.  For this set of experiments I will use a Type-C wall wart connected to the Cypress 4533 BCR development kit to supply power.

Test the BCR

The first thing that I do is connect the whole mess together like this:

Here is how it looks on my desk.  Note that the Keithey can measure current and voltage… but that I don’t have a way in this setup to measure either the voltage/current from the power supply or the current out of the CY4533

I step the output load from 1A to 12A in 1A increments.  I am super happy to see that the output voltage of the IR3894 is perfectly regulated to 1.198V.  It is also interesting to see that the Type-C power supply is able to keep the voltage within 3.25% of nominal even when I am using 12A on the IRDC3894 output (probably around 1.5A from the Type-C)

Measure the Input Current

In the previous article I used the current measurement from the Keithley bench top power supply.  In the setup above I don’t have a way to measure the actual input current.  To fix this put my new Keithley DAQ6510 in series with the IRDC3894 board.  Like this:

Then I step through the 1A-12A load conditions.  Once again the IR3894 provide a very well regulated voltage and current (exactly the same as before so I didn’t write them down)

Here is a table with the data from the previous post (without the Type-C power supply) versus the Type-C power supply.

2230-30-1 Power Supply With 6510 current meter in input path
Vin Iin Win Vout Iout Wout Eff Vin Iin Win Eff-C Loss
12 0.27 3.24 1.198 0 0 0%
12 0.129 1.548 1.198 0.998 1.195604 77% 11.91 0.129 1.53639 77.8% -0.6%
12 0.239 2.868 1.198 1.998 2.393604 83% 11.8 0.242 2.8556 83.8% -0.4%
12 0.345 4.14 1.198 2.998 3.591604 87% 11.7 0.352 4.1184 87.2% -0.5%
12 0.454 5.448 1.198 3.998 4.789604 88% 11.59 0.467 5.41253 88.5% -0.6%
12 0.564 6.768 1.198 4.999 5.988802 88% 11.47 0.586 6.72142 89.1% -0.6%
12 0.677 8.124 1.198 5.998 7.185604 88% 11.36 0.709 8.05424 89.2% -0.8%
12 0.792 9.504 1.198 6.998 8.383604 88% 11.25 0.837 9.41625 89.0% -0.8%
12 0.909 10.908 1.198 7.998 9.581604 88% 11.13 0.97 10.7961 88.8% -0.9%
12 1.029 12.348 1.198 8.998 10.779604 87% 10.95 1.115 12.20925 88.3% -1.0%
12 1.152 13.824 1.198 9.999 11.978802 87% 10.85 1.258 13.6493 87.8% -1.1%
12 1.277 15.324 1.198 10.998 13.175604 86% 10.8 1.401 15.1308 87.1% -1.1%
12 1.406 16.872 1.198 11.997 14.372406 85% 10.68 1.558 16.63944 86.4% -1.2%

These measurements use 1A/3A range on the Keithley DAQ6510 DMM, which means that they have a 100mΩ shunt resistor in series which drops the voltage by V=IR or about 0.1-ish volts.  This explains most of the difference from the Power Supply to the Type-C setup.

It is actually very interesting to look at the data to see the impact of lowering the input voltage on the efficiency of the IR3894.  It appears that at the highest load and lowest input voltage the efficiency is down by 1.2%

Watch the Sunrise

While I was sitting there at my desk thinking about what to do next, I decided that the best thing to do was go sit in my hottub and watch the sunrise on God’s country.

USB C Power Meter Tester

I was hoping to be able to measure the input current and voltage from the Type-C power supply so that I could calculate the efficiency of the CY4533 EZ BCR.  And as a result the efficiency of the whole system.  There wasn’t a place on the Type-C development kit to make these measurements, but the Cypress Apps manager for Type-C – Palani – said I should buy something like this from Amazon.

 

So I did.  You can plug it into Type-A or Type-C and it will tell you how much V/I are coming out.  In the picture below you can see 20.4v@0.11A

Even better it has a handy-dandy mode where it can display Chinese?

Here is a picture in my actual setup:

And a picture of the whole crazy setup.

Now I step through my 12 load conditions from 1A to 12A and record the V/I from the Fluke and the USB Power Tester.

Here is the data in table form with power and efficiency added.

Type C Power Tester
Vin Iin Win Eff-No Meter
11.99 0.15 1.7985 66.5%
11.95 0.26 3.107 77.0%
11.92 0.36 4.2912 83.7%
11.88 0.48 5.7024 84.0%
11.85 0.59 6.9915 85.7%
11.82 0.7 8.274 86.8%
11.79 0.82 9.6678 86.7%
11.75 0.94 11.045 86.8%
11.71 1.07 12.5297 86.0%
11.68 1.2 14.016 85.5%
11.64 1.33 15.4812 85.1%
11.6 1.46 16.936 84.9%

Next, I plot the new data with the previous two plots.  Obviously, it is screwed up.  I would bet money that the data points at 2A, 4A and 12A are wrong.  But, I don’t think that it is worthwhile to take steps to figure out the real current.  So, I suppose that is what you get from a $19 power meter.

Efficiency of CY4533 EZ-PD BCR

I had really wanted to measure the efficiency of the BCR setup.  To do that I needed to be able to measure the output power (V/I) and the input power (V/I).  Unfortunately the power meter doesn’t seem to be very good… so I suppose that I will have to wait to build my real board where I can install some power jumpers the real numbers.

Cypress Type-C Barrel Connector Replacement + Infineon Buck DC/DC (Part 2)

Summary

In this article I will show you how to use a Keithley 2380 (actually two different ones) to test the output of the IRDC3894 12V->1.2V 12A buck development kit.

The Story

To this point I have written several articles about my process of designing a power supply for my new IoT device.  It needs to provide for quite a bit of power, actually 60W is what I am planning on.  I really wanted to make sure that the IR3894 chip would do what it says it would, specifically supply 12A.  The development kit is pretty simple.  There are two banana plug to  provide power to Vin and two banana plus for the load.

For this round of tests I will Keithley 2230-30-1 to provide power and I will use my Keithley 2380-120-60 to serve as the load.

The two mini grabbers are attached to to remote sensing terminals on the Keithley 2380.

After I had it all hooked up I went in 1A increments from 0 to 12A, then I went in 0.1A increments until I ran out of input power.

Here is the actual data table.  Note that I added columns to show the calculated input power.  And I calculated the efficiency of the system Wout/Win

Vin Iin Win Vout Iout W Eff
12 0.27 3.24 1.198 0 0 0%
12 0.129 1.548 1.198 0.998 1.195604 77%
12 0.239 2.868 1.198 1.998 2.393604 83%
12 0.345 4.14 1.198 2.998 3.591604 87%
12 0.454 5.448 1.198 3.998 4.789604 88%
12 0.564 6.768 1.198 4.999 5.988802 88%
12 0.677 8.124 1.198 5.998 7.185604 88%
12 0.792 9.504 1.198 6.998 8.383604 88%
12 0.909 10.908 1.198 7.998 9.581604 88%
12 1.029 12.348 1.198 8.998 10.779604 87%
12 1.152 13.824 1.198 9.999 11.978802 87%
12 1.277 15.324 1.198 10.998 13.175604 86%
12 1.406 16.872 1.198 11.997 14.372406 85%
12 1.42 17.04 1.198 12.098 14.493404 85%
12 1.434 17.208 1.198 12.198 14.613204 85%
12 1.448 17.376 1.198 12.297 14.731806 85%
12 1.462 17.544 1.198 12.398 14.852804 85%
12 1.477 17.724 1.198 12.498 14.972604 84%
12 1.49 17.88 1.198 12.59 15.08282 84%

When I plot the data there is something sticking out like a sore thumb.  WTF?  At first I assume that I typed in the wrong number when I transposed the hand written data to the spreadsheet.  So I went and looked at the data table where it appears that I typed it in correctly.  Does the efficiency really have a peak like that?

I decided to go remeasure the 5A datapoint.

Then I looked at my handwritten data sheet where I find that I transposed the last two digits of the input current. (I definitely should automate this measurement)

OK… now the plot looks way better

When I compare the plot from the data sheet versus my data on the same scale (about) they look very similar.  All seems good.