Summary

This article will show you the steps to produce 12A from and IRDC3894.  It also discusses low voltage high current measurement and burden voltage.

The Story

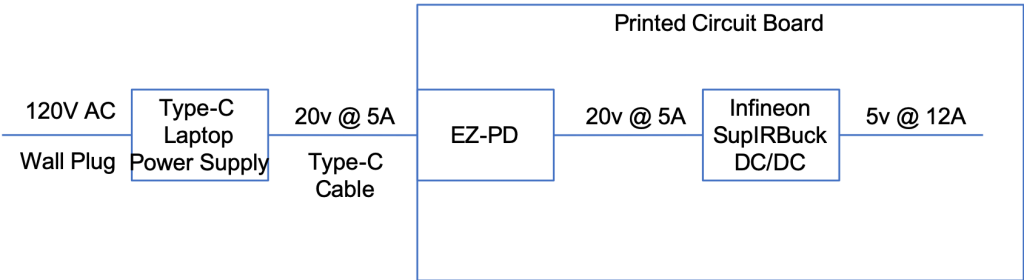
In the last few weeks I have been working on a TypeC to Infineon SupIRbuck power supply that will turn 20V@3A into 5V@12A.

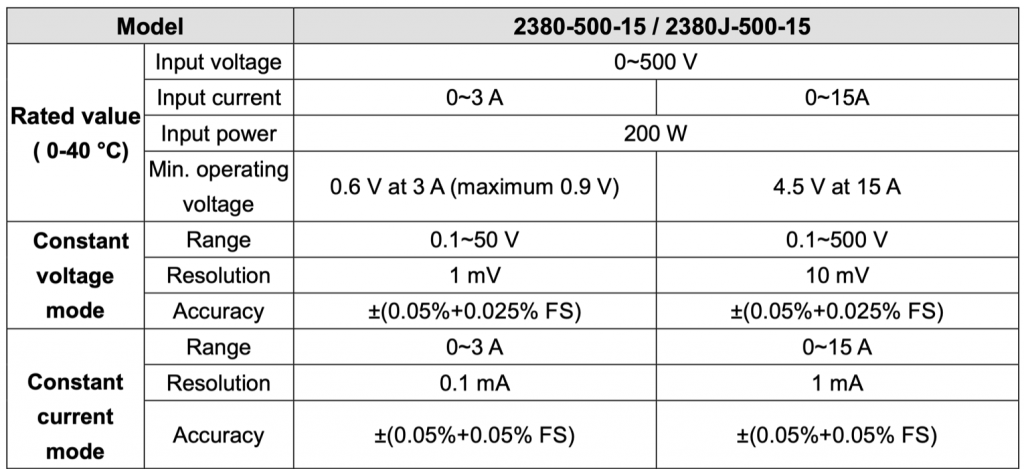
In that process I have been working with a Keithley 2380-500-15 which can act as a load simulator for my design.  The 15 in name means that it can pull 15A which should be more an adequate to test my design.  Unfortunately when I was looking at the specs, I read the part about “15A” but not the part about the “Min Operating Voltage in the 15A range = 4.5V”

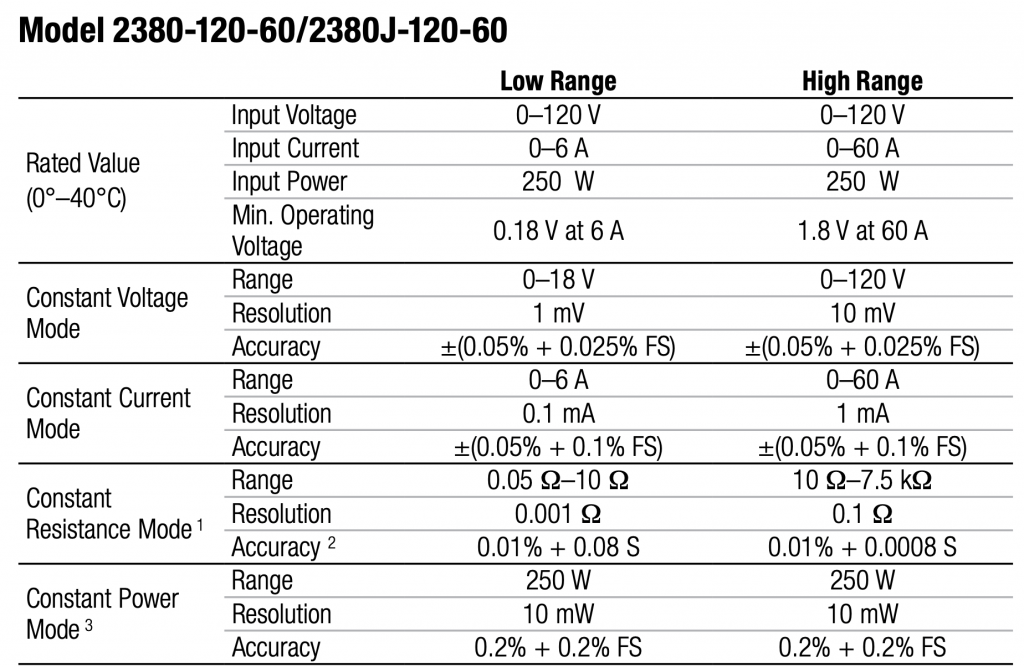
And what I really should have bought (and now have) is a 2380-120-60

Big Resistors

But I really wanted to be able to measure the current coming out of the IR3894.  So, I decided to buy some “Big” resistors.  Well they are not actually high resistance, but they are HIGH power. 35W and 50W.  Unfortunately they are also $4 each.  Here is a 0.33Ω 50W resistor.  (I will totally understand the value of that giant heat sink later on in this article)

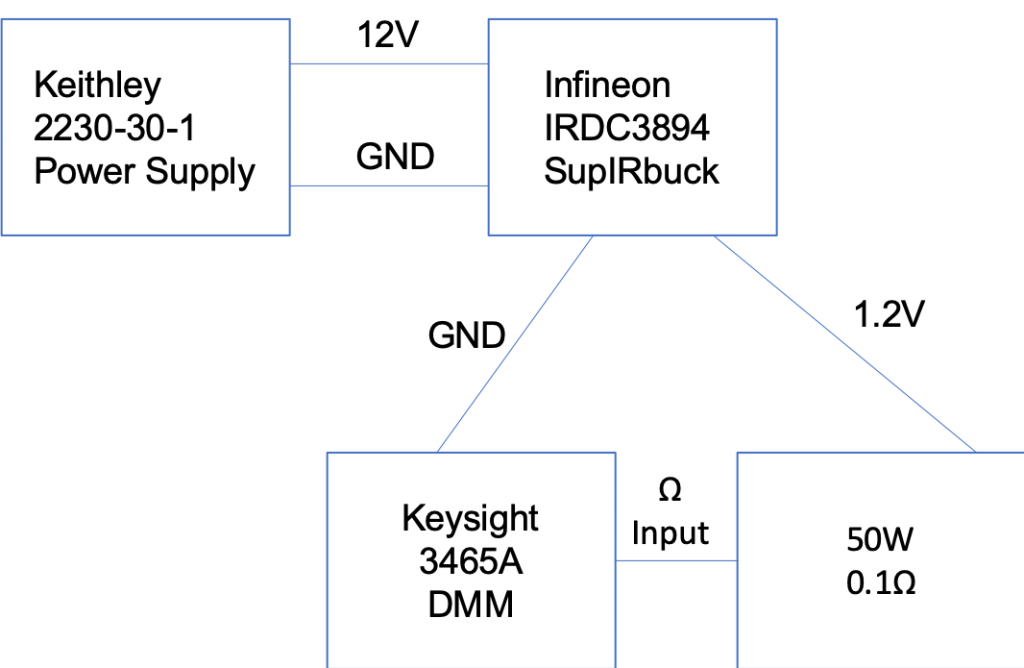
My measurement setup looks like this:

And actually looks like this terrible mess:

Start the measurements

I bought 7 different resistors ranging from 0.1Ω to 1Ω.  This means that I should be able to get something like this table.  Note that the 0.1Ω is marked in red because it exceeds the current limit of my multimeter. (i.e. don’t do that)

V	R	A	W	Rating
1.2	0.10	12.0	14.4	35
1.2	0.15	8.0	9.6	50
1.2	0.20	6.0	7.2	35
1.2	0.33	3.6	4.4	50
1.2	0.50	2.4	2.9	35
1.2	0.75	1.6	1.9	50
1.2	1.00	1.2	1.4	50

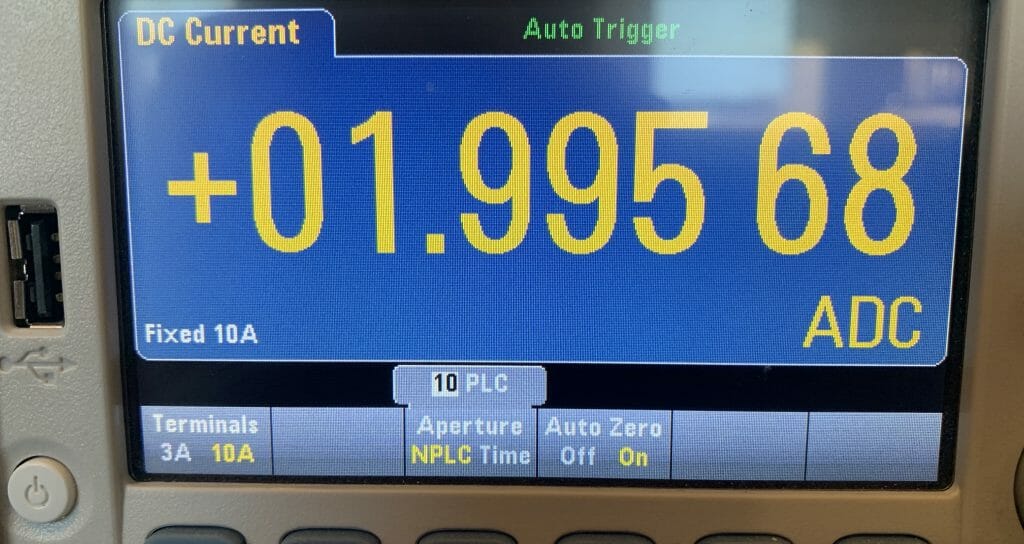
I wasn’t exactly sure what was going to happen so I decided to start with the 0.33Ω resistor

I was hoping to get 1.2V/0.33Ω = 3.6A yet I end up with 1.99A where is my other 1.6A?

I put in a 0.1Ω, 0.15Ω and 0.75Ω and measured the current.  Then I calculate the effective resistance of the system and it turns out that there is essentially another 0.27Ω in series with my R1

V=I(R1+Rb)

V/I-R1 = Rb

V	A	R1Ω	RbΩ	R1+RbΩ
1.2	2.0	0.33	0.27	0.60
1.2	3.16	0.10	0.28	0.38
1.2	2.85	0.15	0.27	0.42
1.2	1.175	0.75	0.27	1.02

Where in the world is the other 0.27Ω?

Melt the Probe

This leads me to the great idea that is just the lead wires, and that I ought to just pull out the resistor and see what happens.  Well, what happens is that I melt the probe, and I still don’t get numbers that make sense.

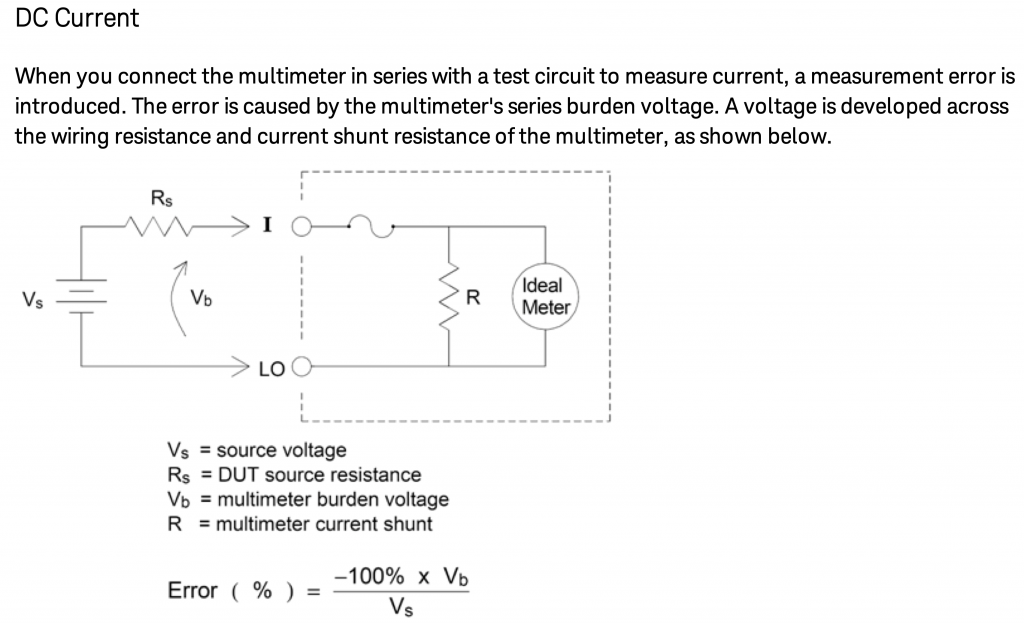
Burden Voltage

The real story is, of course, that digital multimeters are hardly “ideal” and that when you are measuring current what you are really doing is measuring the voltage across a “shunt resistor”.  A shunt resistor is just a small valued highly precise resistor.  The voltage across this resistor is also known as the burden voltage (which is why I called it Rb above).  Here is a picture out of the Keysight documentation.

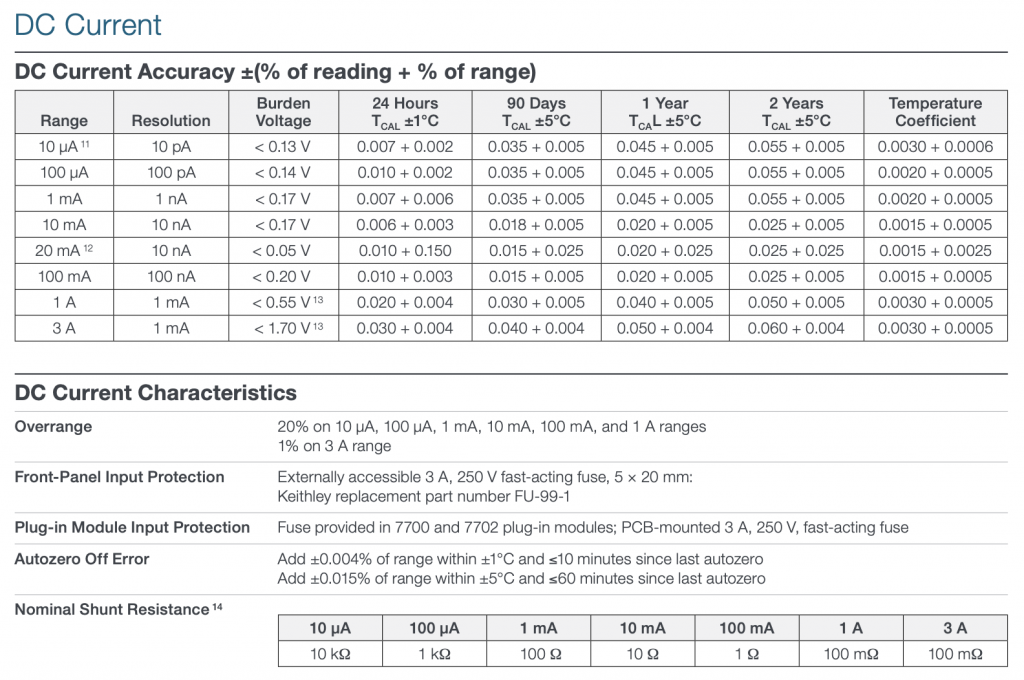
But how big is that resistor?  Well, unfortunately it is not specified directly in the documentation.  But, when you look at the data sheet you find that the maximum burden voltage is 0.5V at 10A.

This means that shunt resistor is no more than 0.5v/10A=0.05Ω.  I just ordered a new Keithley DAQ6510 Digital Acquisition System Multimeter (which Im very excited about) that has the following table in documentation where it says the shunt resistor is 100mΩ for the 3A range.

Measure the Lead Resistance

So now we know that the shunt resistor is something like 0.05Ω.  That means the rest of the resistance has to be in the test setup.  So

V=(R1 + Rl + Rb)*I … the lead resistance + the shunt resistor + the actual resistor.  I go ahead and calculate what the lead resistance with several different resistors.

This means the resistance of my lead wires must be something like 0.23Ω

V	A	R1	Rl	Rb	R1+Rb+Rl	VR1	VRl	VRb
1.2	2.00	0.33	0.23	0.04	0.37	0.66	0.46	0.08
1.2	3.16	0.10	0.23	0.04	0.15	0.32	0.73	0.16
1.2	2.85	0.15	0.23	0.04	0.19	0.43	0.66	0.12
1.2	1.18	0.75	0.23	0.04	0.79	0.88	0.27	0.05

Again I start to look for the lead wire resistance … 0.6Ω for the melted lead.  Curious.

It is pretty easy to get some crazy measurements.  2.7Ω just pushing two banana plugs together (though you can see it blinking)

If I measure the red banana plug wire looped back the measurement is 0.016Ω – OK that is pretty small

And the black one is almost the same.

After some experimenting mixing and matching cables together the lowest I manage to get in a configuration that I can actually plug together is 0.15Ω which gave me 7.8A.

So where does this leave me?  To tell you the truth it leaves me a bit frustrated.  I really wanted to get 12A out of my setup (which is what it should be able to do).  But the most I can safely measure is 10A.  And the lowest combination of resistors I seem to be able to get is 0.15Ω.  So I decide to solder the 0.1Ω resistor straight into the board and see what happens. (yes that is some ugly soldering)

And now Im really frustrated because when I turn on the bench power supply I get 9.9V and 0.6A … even though it is set for 12V

And when I look at the output voltage I get 0.4V.  Which means it isn’t working.  Why?  I don’t know…. which is beyond annoying.  Walk away now I say to myself (actually that was my wife yelling at me 🙂 )

24 Hours Later

After sleeping on it, I remember that the Enable pin is used as an “Under Voltage Lock Out”.  The purpose of the UVLO is to not turn on until the input voltage has enough power to supply the system.  Given that I am am asking for 12A I realize… maybe I need to “enable” later in the power supply voltage rise.

So what I do I solder in a jumper to “Enable” then I press fit it into the ground.  Then turn on the power supply.  I measure the output as 0V.  That is good.  Then pull the enable jumper wire and let the IR3894 turn on.

Sure enough.  When I look at the input it gets to 12V@1.4A and the output is still steady at 1.2v.  And my 0.1Ω is very hot.  I suppose that heatsink tab is there for a  reason.

I know from Ohms law that I am getting 12A@1.2V.  So the IR3894 seems to do the trick!